[1] R. Szeliski. Computer Vision: Algorithms and Applications[M]. 2010.

[2] 塞利斯基, 艾海舟. 计算机视觉:算法与应用[M]. 清华大学出版社, 2012.

1 Geometric primitives and transformations 几何基元和变换

1.1 Geometric primitives 几何基元

2D点

2D点可以用一对数值来表示：\(\boldsymbol{x}= (x, y) \in \mathcal{R}^2\)，

也可以用齐次坐标（homogeneous coordinates）表示：\(\widetilde{\boldsymbol{x}}=(\widetilde{x}, \widetilde{y}, \widetilde{w}) \in \mathcal{P}^2 ​\)。其中，\(4\mathcal{P}^2 = \mathcal{R}^3 - (0, 0, 0)​\)表示2D投影空间（2D projective space）。

齐次矢量\(\widetilde{\boldsymbol{x}}\)通过除以最后一个元素\(\widetilde{w}\)转换为非齐次矢量\(\boldsymbol{x}\)：\(\widetilde{\boldsymbol{x}} = (\widetilde{x}, \widetilde{y}, \widetilde{w}) = \widetilde{w}(x, y, 1) = \widetilde{w} \overline{\boldsymbol{x}}\)。其中，\(\overline{\boldsymbol{x}} = (x, y, 1)\)是增广矢量（augmented vector）。

2D直线

齐次坐标\(\widetilde{\boldsymbol{l}} = (a, b, c)\)可以用来表示直线方程：\(\overline{\boldsymbol{x}} \cdot \widetilde{\boldsymbol{l}} = ax + by + c = 0\)；

两条直线的交点：\(\widetilde{\boldsymbol{x}} = \widetilde{\boldsymbol{l}}_1 \times \widetilde{\boldsymbol{l}}_2\)；

连接两点的直线：\(\widetilde{\boldsymbol{l}} = \widetilde{\boldsymbol{x}}_1 \times \widetilde{\boldsymbol{x}}_2\)

利用最小二乘法（least squares）可以求得多条直线的交点或多个点拟合出来的直线。

2D圆锥曲线（conics）

圆锥曲线可以用二次方程写为：\(\widetilde{\boldsymbol{x}}^T Q \widetilde{\boldsymbol{x}} = 0\)。这在多视角几何（multi-view geometry）和摄像机标定（camera calibration）中十分重要。

3D点

同理，3D点可以写为非齐次坐标：\(\boldsymbol{x}= (x, y, z) \in \mathcal{R}^3\)，

也可以用齐次坐标表示：\(\widetilde{\boldsymbol{x}}=(\widetilde{x}, \widetilde{y}, \widetilde{z}, \widetilde{w}) \in \mathcal{P}^3\)。

增广矢量\(\overline{\boldsymbol{x}} = (x, y, z, 1)\)可以用来表示3D点：\(\widetilde{\boldsymbol{x}} = \widetilde{w} \overline{\boldsymbol{x}}\)。

3D平面

齐次坐标\(\widetilde{\boldsymbol{m}} = (a, b, c, d)\)可以用来表示平面方程：\(\overline{\boldsymbol{x}} \cdot \widetilde{\boldsymbol{m}} = ax + by + cz + d = 0\)；

3D直线

使用直线上的两个点\((\boldsymbol{p}, \boldsymbol{q})\)的线性组合\(\boldsymbol{r} = (1-\lambda) \boldsymbol{p} + \lambda \boldsymbol{q}\)，这里限定\(0 \le \lambda \le 1\)；

使用齐次坐标可以将直线写为：\(\widetilde{\boldsymbol{r}} = \mu \widetilde{\boldsymbol{p}} + \lambda \widetilde{\boldsymbol{q}}\)。

这种表达方式的缺点是自由度太多（6而不是4）。

使用Plücker coordinates只有4个自由度：\(\boldsymbol{L} = \widetilde{\boldsymbol{p}} \widetilde{\boldsymbol{q}}^T -\widetilde{\boldsymbol{q}} \widetilde{\boldsymbol{p}} ^T\)，\(\widetilde{\boldsymbol{p}}\)和\(\widetilde{\boldsymbol{q}}\)是直线上任意非等同的两点。\(\boldsymbol{L}\)还应该满足\(det(\boldsymbol{L}) = 0\)，这产生了一个二次约束。

3D二次曲面（quadrics）

类比圆锥曲线可以写出二次曲面方程：\(\widetilde{\boldsymbol{x}}^T Q \widetilde{\boldsymbol{x}} = 0\)。

1.2 2D transformations 2D变换

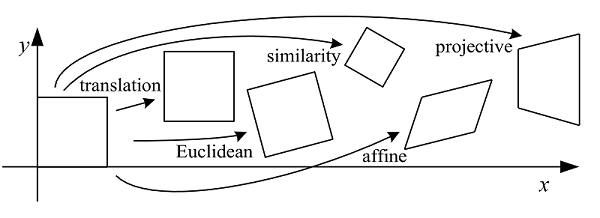
2D变换包括平移（translation）、欧式变换（Euclidean，旋转加平移）、相似（similarity，放缩旋转）、仿射（affine）、投影（projective）。

平移

可以写作\(x' = x + t\)；

或者\(x' = \left[ \begin{matrix} \boldsymbol{I} & t \end{matrix} \right] \overline{x}​\)。其中，\(\boldsymbol{I}​\)是​\(2 \times 2​\)的单位矩阵。

或者\(\overline{x}' = \left[ \begin{matrix} \boldsymbol{I} & t \\ 0^T &1 \end{matrix} \right] \overline{x}​\)。用\(3 \times 3​\)矩阵取代\(2 \times 3​\)矩阵表达可以使变换链成为可能。

欧式变换（旋转加平移）

可以写作\(x' =\boldsymbol{R} x + t​\)；

或者

\[x' = \left[ \begin{matrix} \boldsymbol{R} & t \end{matrix} \right] \overline{x}\]

其中

\[\boldsymbol{R}= \left[ \begin{matrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{matrix} \right]\]

是一个正交旋转矩阵，满足\(\boldsymbol{R}\boldsymbol{R}^T=\boldsymbol{I}\)且$$\left

\boldsymbol{R}\right

= 1$$。

相似变换（放缩旋转）

可以写作\(x' = s \boldsymbol{R} x + t​\)；

或者

\[x' = \left[ \begin{matrix} s\boldsymbol{R} & t \end{matrix} \right] \overline{x} = \left[ \begin{matrix} a & -b & t_x \\ b & a & t_y \end{matrix} \right] \overline{x}\]

可以看出，这里不再要求\(a^2+b^2=1\)。

相似变换中直线间的夹角保持不变。

仿射

可以写作\(x' = \boldsymbol{A}\overline{\boldsymbol{x}}\)。这里\(\boldsymbol{A}\)是\(2 \times 3\)矩阵。

或者

\[x'= \left[ \begin{matrix} a_{00} & a_{01} & a_{02} \\ a_{10} & a_{11} & a_{12} \end{matrix} \right] \overline{x}\]

仿射变换下平行关系保持不变。