Problem Formulation
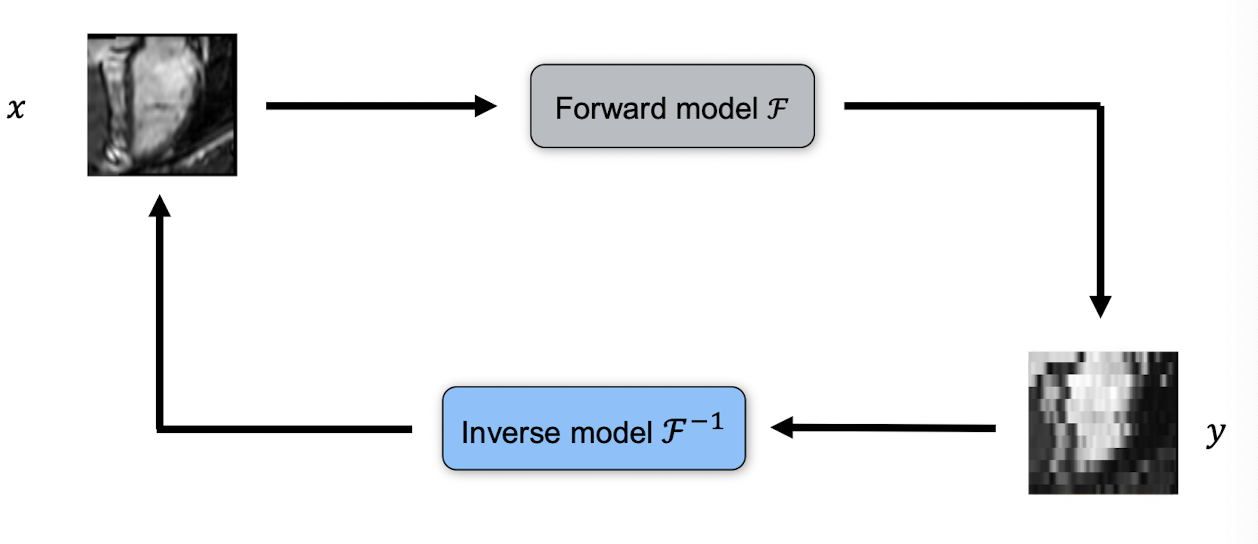
Forward model \(y = A x + n\)
- Goal: recover \(x\) from noisy measurements \(y\)
- Applications: inpainting, deblurring, denoising, super-resolution, reconstruction, registration
Classical Approach
Least-squares problem
\(\arg\min_x \mathcal{D}(Ax,y) = \arg\min_x\tfrac12\|A x - y\|^2\) solution \(\hat{x}= (A^T A)^{-1}A^T y\)
ill-posed problem: similar y can leads to wildly different solutions
Regularization
\(\arg\min_x \mathcal{D}(Ax,y)+\lambda\mathcal{R}(x)\) where \(\mathcal{D}(Ax,y)\) data consistency term, \(\mathcal{R}(x)\) regularisation term (encoding prior knowledge on \(x\)), \(\lambda\) regularisation parameter.
Common regularisers
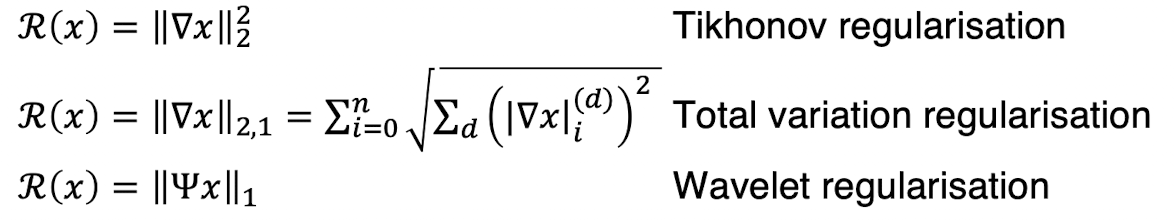
ML Approach
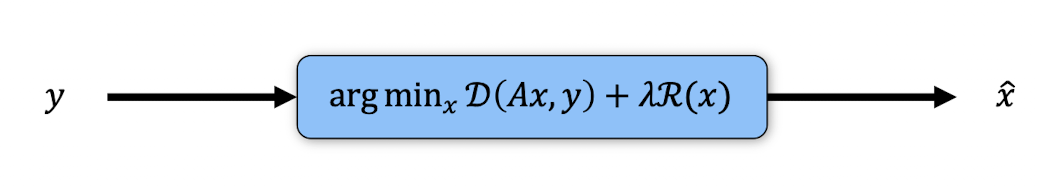 Instead of choosing \(\mathcal{R}\) a-priori based on a simple model of image, learn \(\mathcal{R}\) from training data.
Instead of choosing \(\mathcal{R}\) a-priori based on a simple model of image, learn \(\mathcal{R}\) from training data.
Forward & Inverse Models
 Inverse model \(\mathcal{F}_\phi^{-1}\): directly map \(y\to x\) via a trained network.
Inverse model \(\mathcal{F}_\phi^{-1}\): directly map \(y\to x\) via a trained network.
Method Taxonomy
Model-agnostic
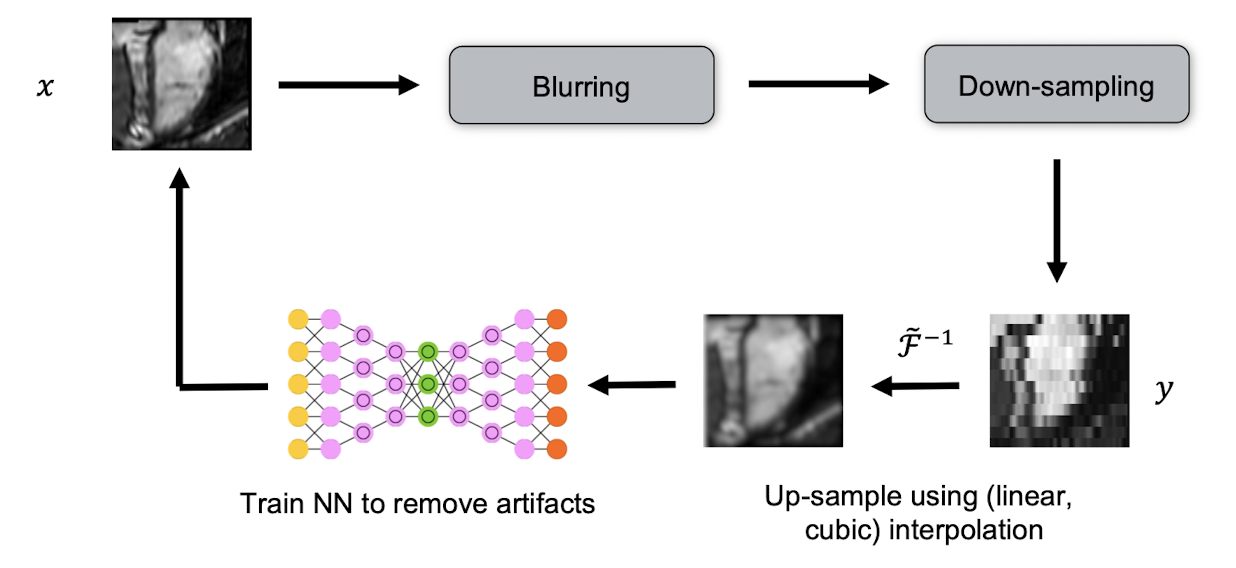
- Ignore \(A\), learn \(y\to x\) directly
- Example: Up-sampling
Decoupled
- Learn denoiser or prior, then plug into classical solver (plug-and-play)
- Example: Deep proximal gradient -> unroll proximal gradient steps, replace proximal operator with learned denoiser
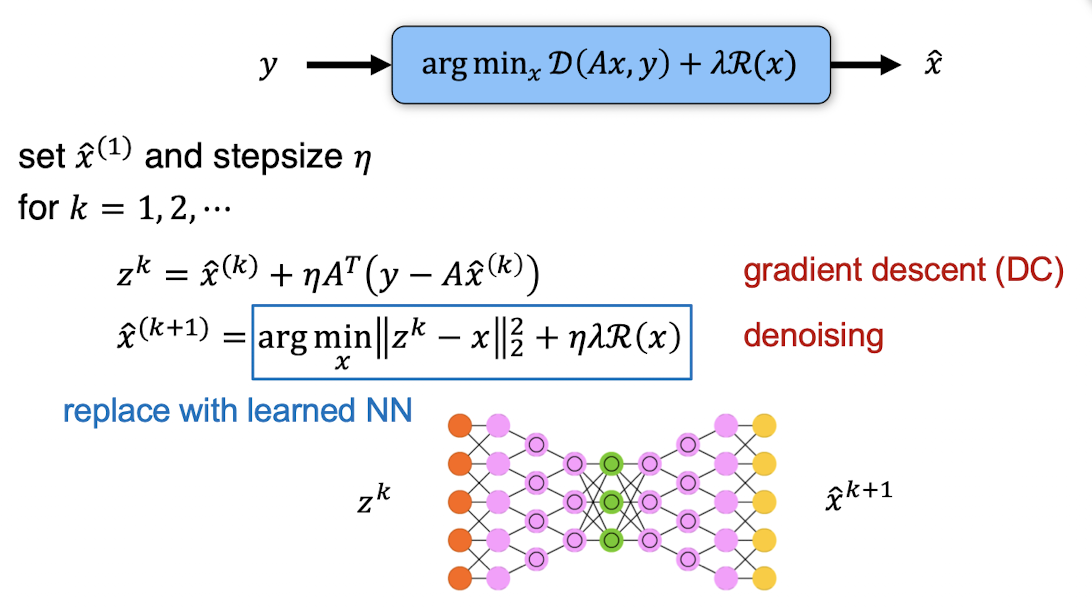
- Example: GANs -> constrain \(x\) to lie in generator manifold \(\mathcal G(z)\), solve \(\min_z\|y - A\mathcal G(z)\|\)

Unrolled Optimization
- Embed iterative solver steps into a network and learn updates
- Example: Gradient Descent Networks -> unroll gradient descent and learn components Assume R(x) is differentiable
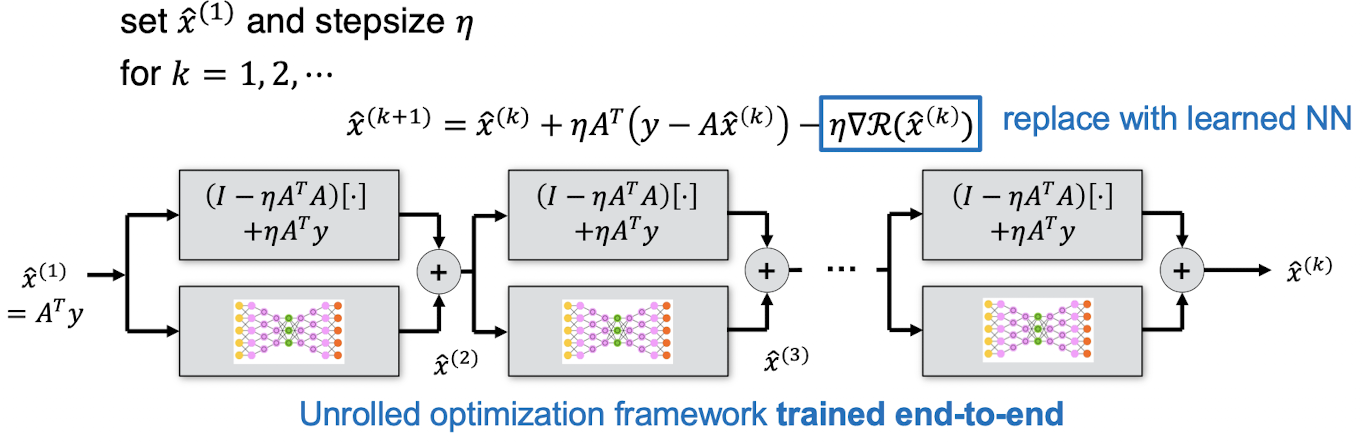
Image Super-Resolution
Problem formulation: Upsample low-resolution (LR) image to high-resolution (HR or SR)
Common Super-Resolution Frameworks
Post-upsampling: (interpolate)
- directly upsample LR image into SR with learnable upsampling layers
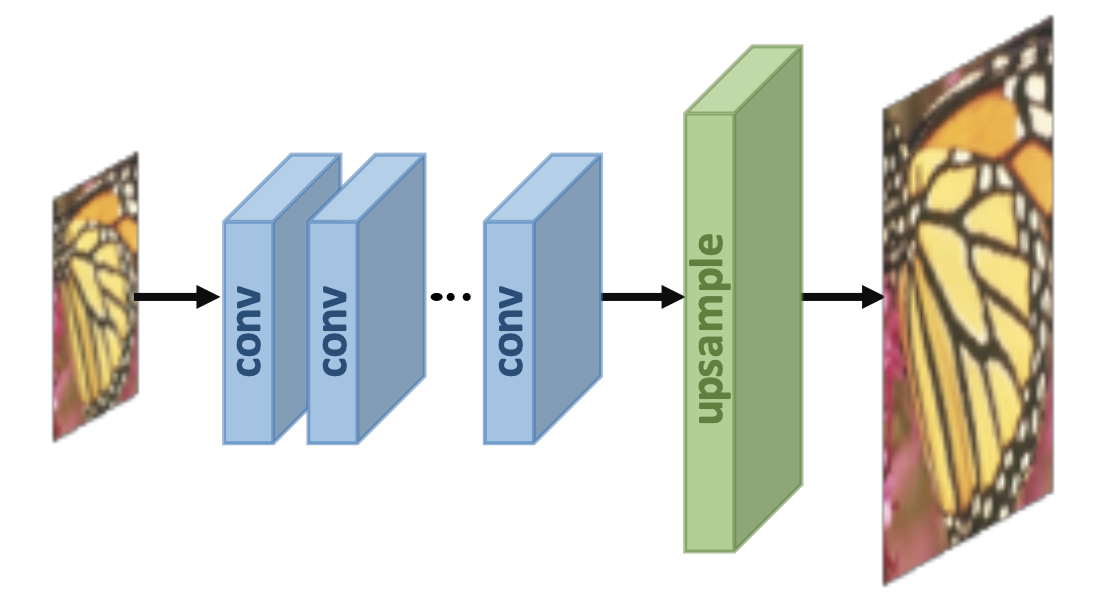
- fast, low memory
- has to learn entire upsampling pipeline
- limited to a specific up-sampling factor
Pre-upsampling: two-stage process (interpolate then refine)
- First use traditional upsampling algorithm (e.g. linear interpolation) to obtain SR images; Then refining upsampled using a deep neural network (usually a CNN)
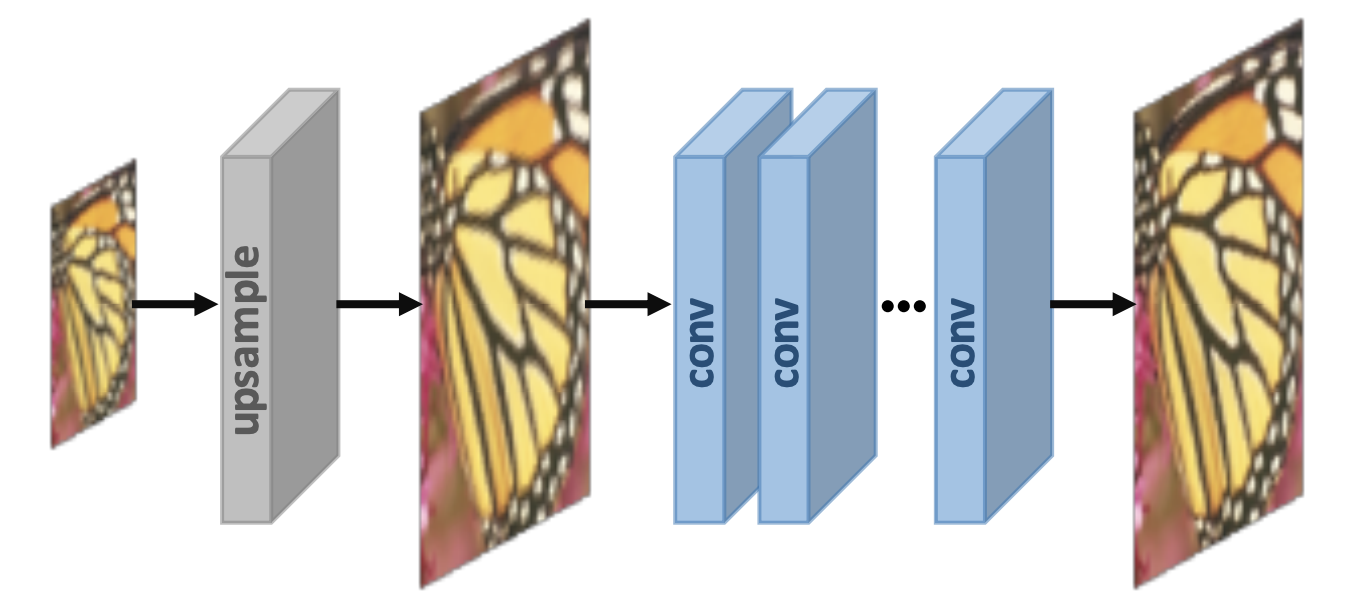
- flexible scaling,
- higher compute and memory
Progressive Upsampling: multi-stage process (gradual resolution increase)
- Use a cascade of CNNs to progressively reconstruct higher-resolution images.
- At each stage, the images are upsampled to higher resolution and refined by CNNs
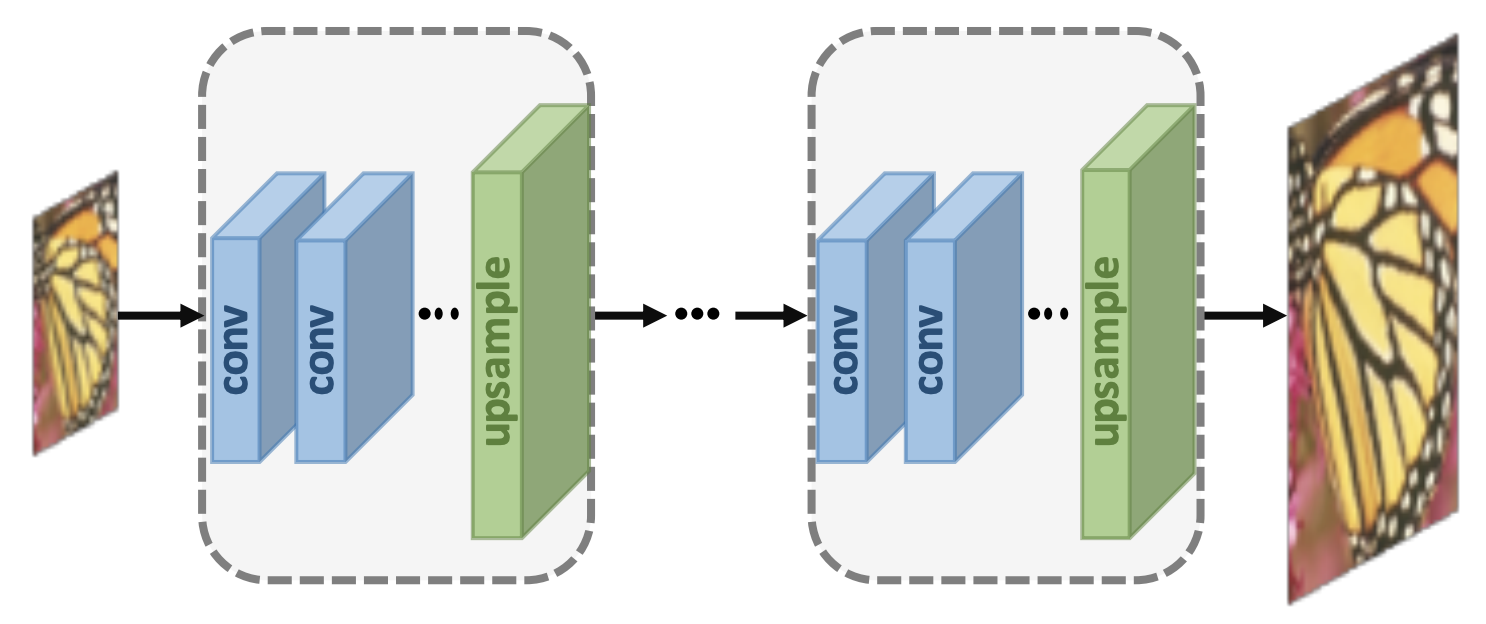
- Decomposes complex task into simple tasks
- Reasonable efficiency
- Sometimes difficult to train very deep models
Iterative Back-Projection: alternate for error feedback
- Alternate between upsampling and downsampling (back-projection) operations
-
Mutually connected up- and down-sampling stages
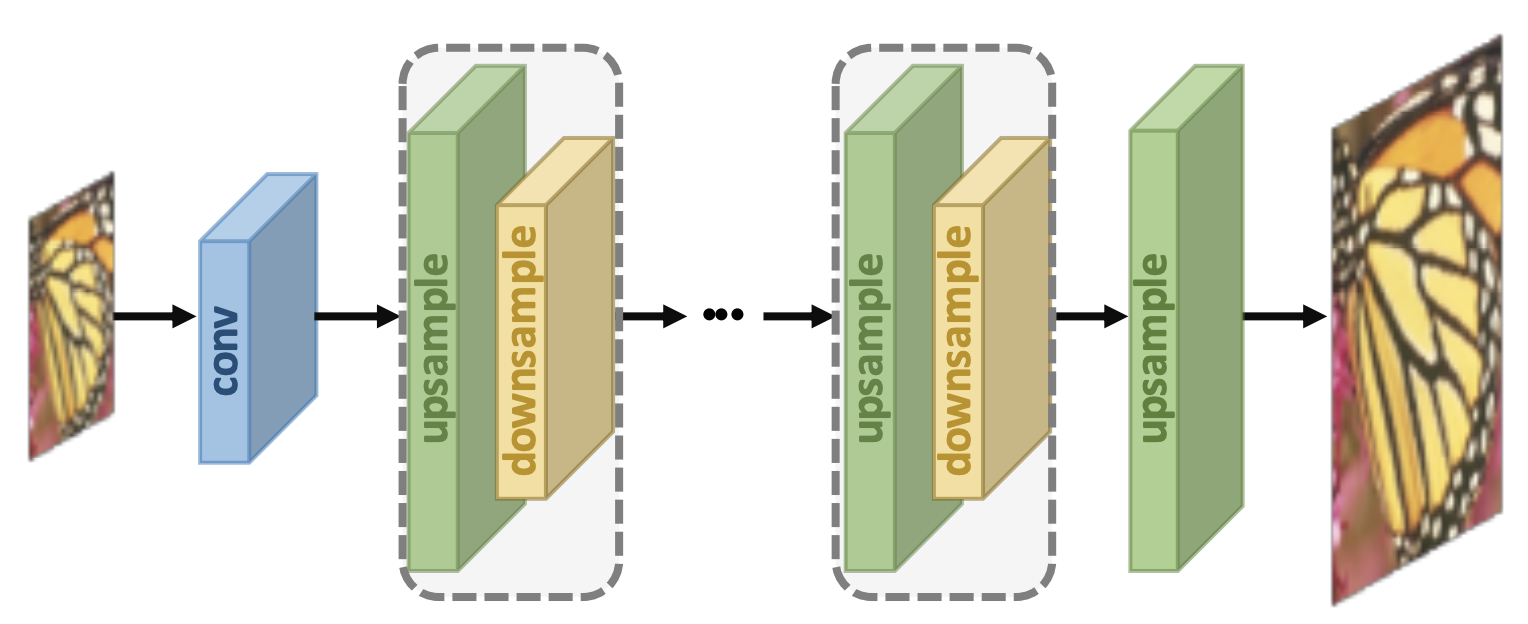
- Superior performance as it allows error feedback
- Easier training of deep networks
Losses pixel-wise (L1/L2, Huber), perceptual (VGG features), total variation, adversarial (GAN)
Deep Image Prior
- Idea: a randomly initialized network \(\Psi(z;w)\) fits a single image by optimizing \(w\) on observed pixels
- Applications: denoising, inpainting (solve \(\min_w\|\,(m\odot x) - (m\odot \Psi(z;w))\|^2\))
Image Reconstruction
CT
- high-contrast; high spatial resolution; fast acqiusition; but ionising radiation
- sinogram \(\to\) image via Radon inverse; ill-posed inverse problem under sparse views;
- under-sampled reconstruction to reduce radiation
MRI
- high-contrast; high spatial resolution; no ionising radiation; but slow acquisition process(problematic for moving objects)
- recover image from undersampled k-space (\(y = F x + n\)); aliasing correction needed
- Undersampling patterns:
- low frequency only: blurring; loss of detail
- regular cartesian: coherent wrap-around along PE direction
- variable-density random: incoherent “noise-like” aliasing
- radial: streaks from strong edges
- spiral: off-resonance artifacts at sharpities
- Reconstruction approaches
- interpolation in k-space

- deblurring in image space
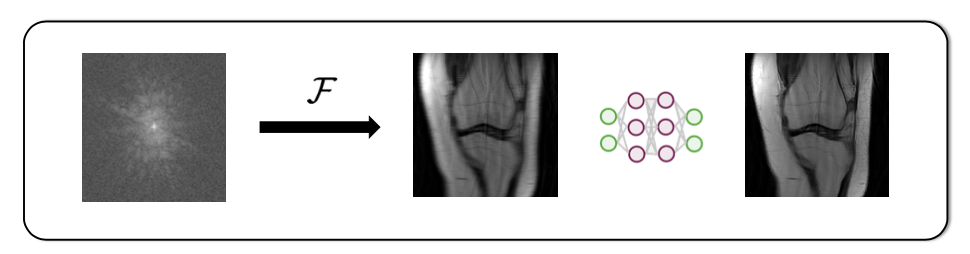
- transform/operator learning
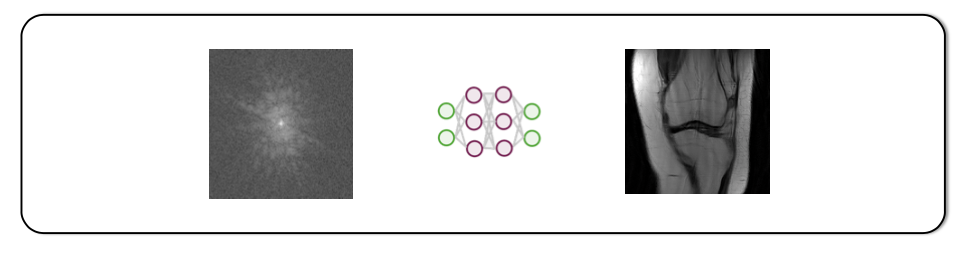
- interpolation in k-space